第9回 関数と再帰#
この授業で学ぶこと#
これまでPythonに既に用意されている関数を利用してきたが、今回は自分で関数を定義する方法について学ぶ。関数を定義することによって、繰り返し行われる処理を一箇所に集約し、コードの再利用性を高めるとともに、コードを理解しやすくすることができる。 さらに、関数内で自分自身を呼び出す再帰という手法についても学ぶ。
関数#
関数はdef文により定義する。
Fig. 16 def文の書き方#
関数の定義はヘッダーとブロックから構成される。
ヘッダーには
defの後に関数名を書き、その後のカッコ内に引数を指定する。引数がある場合は、複数の引数をカンマ（
,）で区切って記述する。引数がない場合は、
def 関数名():のようにカッコ内を空欄にする。
ブロックには、その関数が実行する処理を記述する。
return文は、関数から値を返し、同時にその関数の実行を終了するための構文である。
return文は return 戻り値 のように書く。return文が実行されると、指定した戻り値を返して即座に関数の処理を終了する。
return文は省略可能である。return文を省略した場合、関数の処理が最後まで実行された後、自動的に None という値が返される。
第5回で作成したBMIの計算プログラムを例に、関数を作成してみよう。
def bmi(a, b): # aは身長[cm], bは体重[kg]
return 10000 * b / a ** 2
x = bmi(193, 95)
print(x)
関数はreturn文で戻り値を返す。return文がない場合、自動的に None が返される。
def useless_func():
pass
x = useless_func()
print(x)
基本的に、引数は関数定義の順序どおりに渡される。
例えば bmi(193, 95) と呼び出すと、引数は a = 193、b = 95 となるため、関数内部では 10000 * 95 / 193 ** 2 という計算が行われる。
引数を渡す順序を変えたい場合や、引数の一部を省略したい場合には、キーワード引数やデフォルト引数という機能が使える。
キーワード引数を使えば、引数を自由な順序で指定できる。
bmi(b=95, a=193)
デフォルト引数を設定すれば、関数呼び出し時に引数の指定を省略できる。
デフォルト引数は、関数の定義時に次のように 引数名=デフォルト値 という形式で記述する。
def bmi(a=157, b=50):
return 10000 * b / a ** 2
bmi() # a=157, b=50 として計算される
bmi(193, 95) # 引数に値を渡したら、デフォルト値よりこちらが優先される。
スコープ#
スコープとは、変数や関数の名前をプログラム内で参照できる範囲のことである。
主に2つのスコープがある。
グローバルスコープ（モジュールスコープ）
ローカルスコープ
ノートブックを起動するとグローバルスコープが作られる。ノートブックのセル上で変数を定義すると、他のセルからも参照できるのは、これらが同じグローバルスコープに属するためである。ただし関数内はローカルスコープとして独立した範囲になる。
グローバルスコープに属する変数をグローバル変数、ローカルスコープに属する変数をローカル変数という。
以下のコードをもとに、スコープの違いを理解しよう。
a = 1 # グローバル変数
def func():
a = 2 # ローカル変数
print(a)
func() # 出力は 2
print(a) # 出力は 1
上の例で、グローバル変数 a とローカル変数 a は別物である。関数 func() の中で a の値を変更しても、グローバル変数の値には影響しない。
重要な規則として、ローカルスコープからグローバル変数を参照することはできるが、グローバルスコープからローカル変数を参照することはできないというものがある。
b = 1 # グローバル変数
def func():
print(b) # ローカルスコープからグローバル変数 b を参照
func() # 出力は 1
def func():
c = 1 # ローカル変数
func()
print(c) # グローバルスコープからローカル変数 c は参照できないためエラー
スコープは初心者が混乱しやすい概念である。エラーや予期せぬ変数の変化が起きたら、このスコープの規則を思い出して確認するとよい。
turtleによるグラフィック描画#
ここからはturtleというプログラミング学習用のグラフィック描画ライブラリを用いて、関数作成の練習をしてみよう。このライブラリではペン先を表すカメを操作することで、線を描画する。turtleモジュールは外部ライブラリなので、最初にpipによるインストールとimportが必要である。以下のコードを実行することで、turtleモジュールが使用可能な状態になる。
pip install ColabTurtle
import random
import ColabTurtle.Turtle as turtle # Google Colab用のturtleライブラリ
turtle.DEFAULT_PEN_COLOR = 'black'
turtle.DEFAULT_BACKGROUND_COLOR = 'white'
turtleモジュールの主な関数は以下の通りである。
turtle.penup()ペン先を紙から離す。以降は、カメが移動しても線は引かれない。
turtle.pendown()ペン先を紙につける。以降は、カメが移動する度に線が引かれる。
turtle.forward(d)前方に距離 d だけ進む。
turtle.backward(d)後方に距離 d だけ進む。
turtle.goto(x, y)座標(x, y)に移動する。
turtle.position()現在の位置を返す。
turtle.right(a)右方向に a 度回転する。
turtle.left(a)左方向に a 度回転する。
turtle.setheading(a)右方向を0度、下方向を90度とする回転座標で a 度の方向を向く。
turtle.initializeTurtle() を実行すると、初期化により画面が用意される。まずは、画面上の座標について確認してみよう。
turtle.initializeTurtle(initial_window_size=(400, 400))
print(f"現在の座標: {turtle.position()}")
turtle.setheading(0)
turtle.forward(100)
print(f"現在の座標: {turtle.position()}")
turtle.right(90)
turtle.forward(100)
print(f"現在の座標: {turtle.position()}")
画面の大きさはturtle.initializeTurtle() 関数の引数 initial_window_size でタプルを使って指定しており、400 * 400である。
座標は左上を原点(0, 0)とし、x軸は右方向に、y軸は下方向に伸びている。
カメの初期位置は中央の(200, 200)である。
上のプログラムでは、カメはx軸方向に100進んだあと、y軸方向に100進んでいる。
それでは練習問題を通じて、描画用の関数を作ってみよう。
練習1
1辺の長さ size を引数とし、正方形を描画する関数 draw_square() を作成しなさい。
ただし turtle.pendown() から始め、turtle.penup() で終わること。
def draw_square(size):
pass
# 作成したら描画してみる
turtle.initializeTurtle(initial_window_size=(400, 400))
draw_square(100)
練習2
1辺の長さ size を引数とし、正三角形を描画する関数 draw_triangle() を作成しなさい。
ただし turtle.pendown() から始め、turtle.penup() で終わること。
def draw_triangle(size):
pass
# 作成したら描画してみる
turtle.initializeTurtle(initial_window_size=(400, 400))
draw_triangle(100)
練習3
3以上の整数 n および1辺の長さ size を引数とし、正 n 角形を描画する関数 draw_polygon() を作成しなさい。ただし turtle.pendown() から始め、turtle.penup() で終わること。
def draw_polygon(n, size):
pass
# 作成したら描画してみる
turtle.initializeTurtle(initial_window_size=(400, 400))
draw_polygon(5, 100)
練習4
1辺（例えば線分AB）の長さ size を引数とし、星形を描画する関数 draw_star() を作成しなさい。
ただし turtle.pendown() から始め、turtle.penup() で終わること。星形は図の状態から傾いていてもよい。
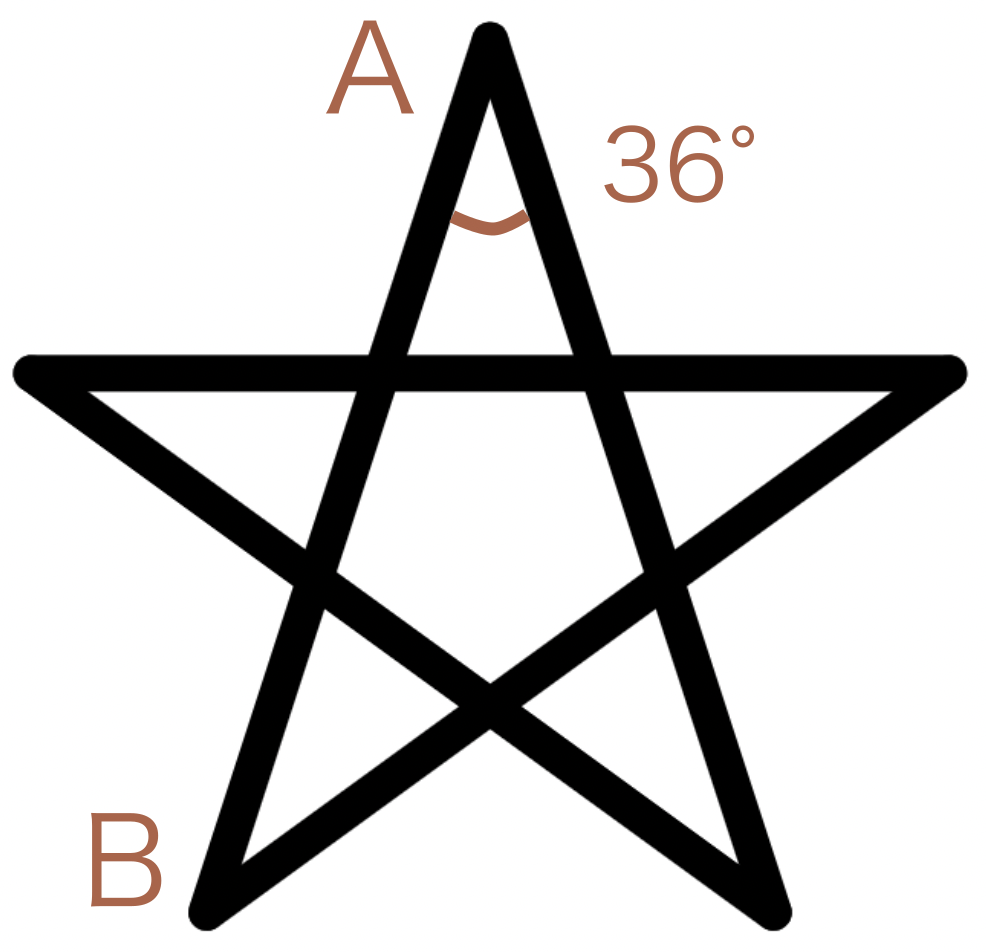
Fig. 17 星形#
def draw_star(size):
pass
# 作成したら描画してみる
turtle.initializeTurtle(initial_window_size=(400, 400))
draw_star(100)
再帰#
以下のコードを実行すると木の枝のような模様が描かれる。どのような処理が行われているか理解できるだろうか。
def draw_branch(length, depth):
turtle.pendown()
if depth == 0:
turtle.forward(length)
else:
turtle.forward(length)
turtle.left(20)
draw_branch(length, depth-1) # 再帰呼び出し
turtle.right(40)
draw_branch(length, depth-1) # 再帰呼び出し
turtle.left(20)
turtle.backward(length)
turtle.penup()
turtle.initializeTurtle(initial_window_size=(400, 400), initial_speed=10) # 描画のスピードを1~13の間で指定できる
turtle.penup()
turtle.goto(200, 350)
# 木を描画
draw_branch(50, 5)
draw_branch() 関数の中身を読むと、draw_branch() 関数自身が呼び出されている箇所がある。
このように関数が自分自身を呼び出すことを再帰呼び出しといい、またそのような定義は再帰的であるという。
このコードを図解すると次のようになる。
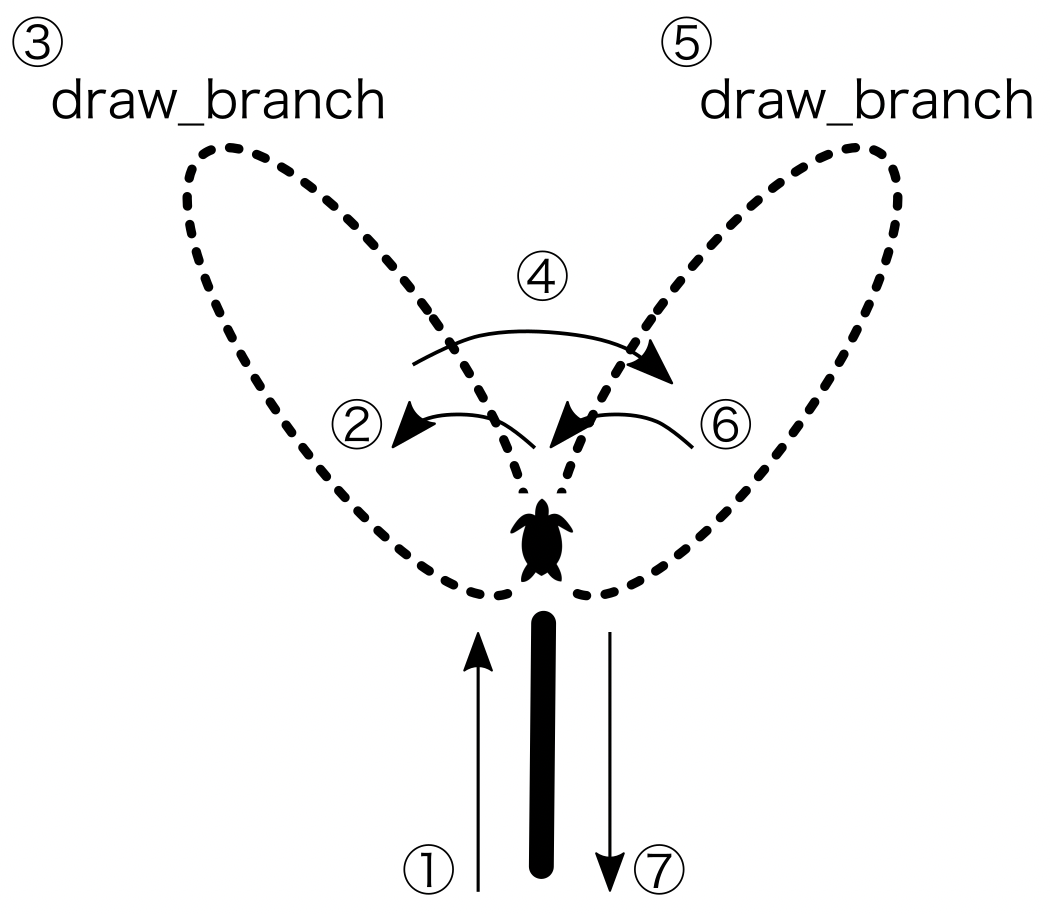
Fig. 18 draw_branc() の再帰呼び出し#
カメはステップ①で木の枝を描き、ステップ③、⑤で再帰的に木を描く。
それ以外は向きの調整と、始点に戻る操作を行っているだけである。
ステップ③、⑤それぞれにおいて、draw_branch() 関数のステップ①〜⑦が繰り返される。
draw_branch() 関数において線を描いているのはステップ①のみであるが、このように繰り返し処理を行うことで、徐々に木の形が出来上がる。
ステップ⑦の始点に戻る操作は、忘れやすい部分ではあるが重要である。 というのもステップ④、⑤は、ステップ③の終了時にカメがちょうど上図の位置にまで戻ってくることを前提としているからである。
再帰を使用することで、for文などの繰り返し構文を用いずに反復的な問題を解くことができる。
ただし、適切に終了条件を設定することが必要であり、これがないと無限ループに陥る可能性がある。
木の例では、枝の深さに制限をつけるため depth という引数を使用し、再帰呼び出しの度に1ずつ減らしている。
そして depth == 0 となったときに再帰呼び出しを行わず、枝を１本描くだけでreturnしている。
練習5
現在の draw_branch() 関数では、木の根元から先端までの分岐の間隔が一定であり、結果として描かれる木は不自然な形状をしている。
より自然な木の形状を再現するために、再帰呼び出しの度に、枝の長さが0.8倍になるように draw_branch() を修正しなさい。
def draw_branch(length, depth):
turtle.pendown()
if depth == 0:
turtle.forward(length)
else:
turtle.forward(length)
turtle.left(20)
draw_branch(length, depth-1)
turtle.right(40)
draw_branch(length, depth-1)
turtle.left(20)
turtle.backward(length)
turtle.penup()
# 作成したら描画してみる
turtle.initializeTurtle(initial_window_size=(400, 400), initial_speed=10)
turtle.penup()
turtle.goto(200, 350)
draw_branch(50, 6)
余談: ジェネラティブ・アート#
余談として、ジェネラティブ・アートについて紹介する。 ジェネラティブ・アートとは、アルゴリズム[1]やルール、自動化されたプロセスを用いて作品を生成するアートの一形態である。 コンピュータやプログラミング言語を使って、これらのアルゴリズムやプロセスを実行し、視覚的または音響的な要素を生み出す。 自然界の複雑さや美しさからインスピレーションを得た作品を、それとは対極の論理的で機械的なコンピュータを使って表現するところが、このアート形態の面白いところである。 したがって、多くの場合に乱数の要素が作品に取り入れられており、実行するごとに毎回異なるパターンを楽しむことができる。
Georg Neesが1968年に発表した Schotter は、最初のジェネラティブ・アート作品だと言われている。 以下のプログラムは、Schotter を模倣したコード[2]である。 12個の正方形が規則的に並べられた行から始まり、下に行くにつれて徐々に秩序が失われる様子が描かれる。
プログラムを実行して鑑賞してみよう。
余力のある人は、どのようなアルゴリズムが使われているか、コードの読解に挑戦してみてほしい。
random.uniform() 関数が初めて使われているが、これは引数を a、bとするとき、a と b の間の小数を一様な確率で返す関数である。
# パラメータ
columns = 12 # 横方向の数
rows = 22 # 縦方向の数
size = 28 # 正方形の一辺の長さ
padding = 2 * size # 余白の大きさ
# 画面の用意
width = columns * size + 2 * padding # 左右の余白の分 2 * padding を足している
height = rows * size + 2 * padding # 上下の...
turtle.initializeTurtle(initial_speed=13, initial_window_size=(width, height))
turtle.hideturtle() # カメは描画しない
# 模様の描画
for y in range(rows):
v = y * (y+1) * 0.11 # yが大きくなるにつれ、乱数を大きくする
for x in range(columns):
rand = random.uniform(-v, v) # 乱数の生成
turtle.penup()
turtle.goto(
padding + x * size + rand * 0.45, # 乱数に0.45を掛けた分だけ位置をずらす
padding + y * size + rand * 0.45
)
turtle.pendown()
turtle.setheading(rand) # 乱数の分だけ傾ける
# 正方形の描画
for _ in range(4):
turtle.forward(size)
turtle.right(90)