第11回 データの可視化#
この授業で学ぶこと#
今回から第13回にかけてデータサイエンスの入門講義を行う。今回はデータの可視化をテーマに、Matplotlibというグラフ描画ライブラリの使い方を学ぶ。またMatplotlibで利用されているNumPyという数値計算ライブラリについて学ぶ。
今後の授業で紹介するコードは何も見ないで書けるようになる必要はなく、これらを雛形にして使えるようになればよい。 Matplotlibを使うと綺麗なグラフを作成できるようになるので、ぜひ他の授業のレポートなどでも活用してみてほしい。
上から順にすべてのセルを実行しましょう
今回以降、ノートブックのコードはNumPyやMatplotlibなど複数のライブラリに依存するため、それぞれのimport文を含むセルを実行していないとどこかでエラーになる。
もし NameError: name 'np' is not defined などのエラーを見かけたら、それより上のセルで実行し忘れているものはないか、とくにimport文を含むものを一通り実行したか確認しよう。
NumPy入門#
NumPyは、数値計算を効率的に行うためのライブラリである。これから学ぶMatplotlibやPandasといったライブラリにおいて数値データを扱うのに用いられる。
NumPyは import numpy によりインポートできる。ただし import numpy as np として np という省略名をつけながらインポートするのが慣例となっている。
import numpy as np
配列#
NumPyでは基本的に ndarray というデータ型を用いる。ndarray は N-dimensional array の略であり、日本語では配列という。配列はリストによく似たデータ型であるが、数値計算を効率的に行うための機能が備わっている。
配列は np.array() 関数にリストを渡すことで、生成することができる。
x = np.array([1.0, 2.0, 3.0])
y = np.array([[1, 2], [3, 4], [5, 6]])
この例では一次元配列、二次元配列を生成している。リストと異なり、配列では要素のデータ型はすべて同じでないといけない。
配列は shape、ndim、size という属性をもち、それぞれ配列の形、次元、要素数を表す。
x.shape
y.shape
x.ndim
y.ndim
x.size
y.size
dtype という属性は、配列の要素のデータ型を表す。NumPyの float64 は組み込み型の float に、int64 は int に対応するデータ型である。
x.dtype
y.dtype
配列の生成方法はリストと np.array() 関数を使った方法の他にも、以下のようなものがある。np.zeros()、np.ones() 関数は、第一引数で指定した形で、それぞれ要素がすべて 0、1 の配列を生成する。
np.zeros((2, 3))
np.ones((1, 2))
np.arange() 関数は、np.arange(start, stop, step) と呼び出すと start から stop までの step 刻みの一次元配列を生成する。
np.arange(0, 1, 0.1)
np.random.normal() 関数は下のように呼び出すと、平均が0で標準偏差が1の正規分布に従う乱数の一次元配列を生成する。
np.random.normal(loc=0, scale=1, size=10)
要素のアクセス#
要素のアクセス方法はリストと似ているが、二次元以上のときに記法が異なる。二次元リストでは data[i][j] というように [] を重ねて要素を指定したが、二次元配列では data[i, j] のように , 区切りで要素を指定する。二次元配列の場合、data[i, j] と指定するときの i の次元を行、j の次元を列という。
print(x[0])
print(y[2, 1])
スライスによって複数の要素にアクセスすることもできる。
z = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(z[1:])
print(z[1:, 1:])
要素の変更は代入文により行う。リストとの違いとして、スライスで指定した複数の要素を一括で変更することもできる。
z[0, 0] = 0
print(z)
z[1:, 1:] = 10
print(z)
演算#
配列には各種演算が定義されており、配列同士の演算を行うことができる。
x = np.array([[1, 2], [3, 4]])
y = np.array([[1, 2], [3, 4]])
x + y
x - y
x * y
x / y
四則演算は基本的に2つの配列の形が揃っていないとエラーになるが、以下のように計算可能なケースもある。
z = np.array([1, 2])
x + z
x * 2
上の例では、足し算を実行する前に z の形を x の形に揃えて np.array([[1, 2], [1, 2]]) と読み替えてから計算が行われる。下の例では、2 を x の形に揃えて np.array([[2, 2], [2, 2]]) と読み替えてから計算が行われる。このような機能をブロードキャストという。
練習1
正の整数 n、m が与えられるとき、形が (n, m) で要素がすべて 0 の二次元配列 data を作成するコードを書きなさい。ただし採点の都合上、print してはいけない。
# n, mの一例
n = 2
m = 2
# 以下にコードを作成し、以下の部分のみ提出する
data = np.zeros((n, m))
練習2
正の整数からなる配列 x が与えられるとき、x の各要素を x の要素の総和で割って得られる配列 p を作成するコードを書きなさい。ただし採点の都合上、print してはいけない。
ヒント:配列の要素の総和は np.sum() 関数によって求められる。
# xの一例
x = np.array([1, 3, 4])
# 以下にコードを作成し、以下の部分のみ提出する
p = x / np.sum(x)
Matplotlib入門#
Pythonでグラフを描画するのにMatplotlibというライブラリがよく用いられる。
Matplotlibを使うには、その中のpyplotというモジュールをimportする。import matplotlib.pyplot as plt として plt という省略名をつけながらインポートするのが慣例となっている。
またグラフのラベルに日本語を使えるようにするためにjapanize_matplotlibというモジュールをimportする。japanize_matplotlibはpipによるインストールが必要である[1]。
pip install japanize_matplotlib
import matplotlib.pyplot as plt
import japanize_matplotlib
plt.rcParams.update({"font.size": 14}) # 文字サイズを14pxとする
まずは描画用のサンプルデータを用意しよう。Matplotlibではリストまたは配列を主に扱う。ここでは配列のデータを用意する。
# 0から10までの0.1刻みの配列
sample_x = np.arange(0, 10, 0.1)
# y = 2x + eps (epsはノイズ)
eps = np.random.normal(loc=0, scale=1, size=len(sample_x))
sample_y = sample_x * 2 + eps
np.arange(0, 10, 0.1) は、0 から 10 までの 0.1 刻みの配列を生成する。したがって、sample_x は要素数100の一次元配列となっている。
len(sample_x)
np.random.normal(loc=0, scale=1, size=len(sample_x)) は、平均が0で標準偏差が1の正規分布に従う乱数の配列を生成する。代入先の eps はデータに加えるノイズとして使用する。
eps[:10] # 先頭の10個を表示
配列は要素ごとの演算を一括で行うことができる。sample_x * 2 + eps により、インデックスごとに sample_x の要素を2倍し、eps の要素を足している。
sample_x[:10]
sample_y[:10]
ここで生成した sample_x と sample_y は \(\varepsilon\) をノイズとして \(y = 2x + \varepsilon\) の関係を満たす2次元データ \((x, y)\) を100個生成したものと見ることができる。
1つ1つのデータは(sample_x[0], sample_y[0]), (sample_x[1], sample_y[1]), …, (sample_x[99], sample_y[99])である。
散布図#
サンプルデータを散布図として可視化してみよう。横軸に \(x\)、縦軸に \(y\) の値をとって各データを点として打って描画する。このことをデータを散布図としてプロットするという。
# プロットの入れ物の用意
fig, ax = plt.subplots(1, 1, figsize=(5, 4))
# 散布図のプロット
ax.scatter(sample_x, sample_y)
# 表示
plt.show()
1行目では plt.subplots() 関数によりFigureオブジェクトとAxesオブジェクトを生成して、変数 fig と ax に代入している[2][3]。
Matplotlibによる描画はFigureオブジェクトとAxesオブジェクト、Axisオブジェクトの3つの要素で構成される。Axisオブジェクトは1つの軸を管理し、Axesオブジェクトは1つのグラフを管理し、Figureオブジェクトは描画全体を管理する。それぞれの関係を次の図に示す。
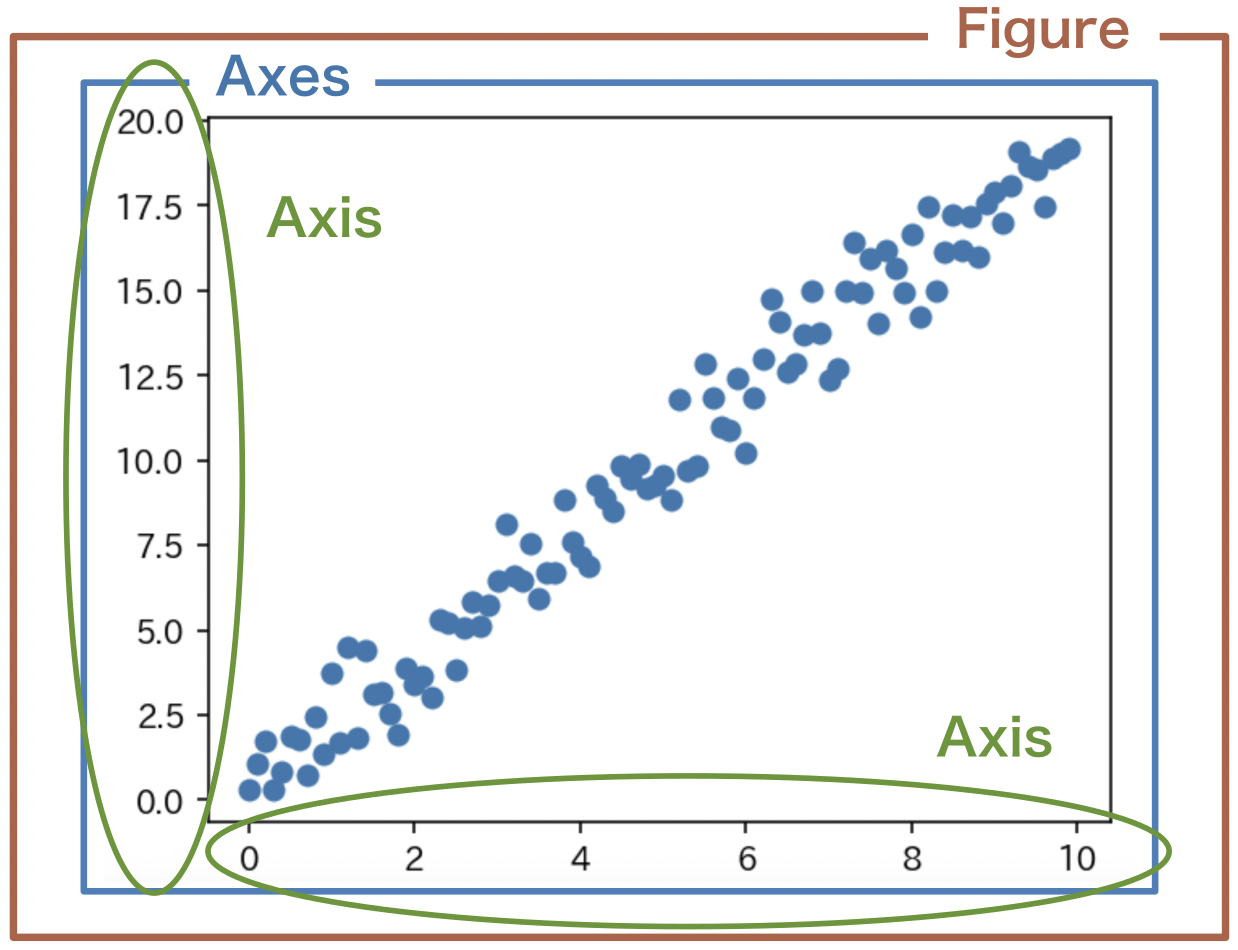
Fig. 22 グラフの構成要素#
plt.subplots() 関数は plt.subplots(n, m, figsize=(w, h)) と呼び出すと、横幅 w、高さ h (単位はインチ)のFigureオブジェクトと、その中に n 行 m 列のn * m 個のAxesオブジェクトを作成する。グラフを1枚だけ描画したい場合は、n = m = 1 と指定する。もしくは引数で何も指定しなければ、デフォルト引数により n = m = 1 が指定される。このときAxesオブジェクトが1つだけ作成され、戻り値の ax はAxesオブジェクトそのものになる。複数のグラフを同時に描画したい場合は、n または m に2以上の整数を指定する。このときAxesオブジェクトが複数作成され、戻り値はAxesオブジェクトの配列となる。
散布図のプロットは ax.scatter() メソッドにより行う。第一引数に横軸の値の配列、第二引数に縦軸の値の配列を指定する。
最後に plt.show() 関数を呼び出すことで、グラフが表示される。
グラフの調整#
次にグラフの見た目を細かく調整してみよう。
まずは1枚のグラフに複数の散布図をプロットする。 先ほどのプロットに \(y = 3x + \varepsilon\) の関係を満たすデータの散布図を追加する。
# プロットの入れ物の用意
fig, ax = plt.subplots(figsize=(5, 4))
# データの用意
sample_y2 = sample_x * 3 + np.random.normal(loc=0, scale=1, size=len(sample_x))
# 散布図のプロット
ax.scatter(sample_x, sample_y)
ax.scatter(sample_x, sample_y2)
# 表示
plt.show()
このように同一のAxesオブジェクトの scatter() メソッドを複数回呼び出すことで、1つのグラフに複数の散布図をプロットすることができる。
プロットの色は自動的に設定されるが、自分で指定することもできる。 凡例や軸ラベル、タイトル、マーカーの種類の設定方法とともに紹介する。
# プロットの入れ物の用意
fig, ax = plt.subplots(figsize=(5, 4))
# 散布図のプロット
ax.scatter(sample_x, sample_y, color="royalblue", marker="v", label="y=2x+e")
ax.scatter(sample_x, sample_y2, color="forestgreen", marker="x", label="y=3x+e")
# 軸ラベル・タイトルの設定
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_title("xとyの関係")
# 表示
plt.legend() # 凡例の表示
plt.show()
ax.scatter() メソッドのキーワード引数を使って、color を設定すると色を変更できる(color で指定できる色の名前の一覧はこちら)。marker を設定するとマーカーの種類を変更できる(marker で指定できる値の一覧はこちら)。label を設定すると凡例の表示を設定できる。凡例を表示するには、最後に plt.legend() を呼び出す。
軸ラベルは ax.set_xlabel()、ax.set_ylabel() により設定する。同様にタイトルは ax.set_title() により設定する。
折れ線グラフ#
散布図と並んでよく使われるのが折れ線グラフである。折れ線グラフでは、基本的にデータの順番は \(x\) の値について昇順または降順であることを仮定する。 このとき横軸に \(x\)、縦軸に \(y\) の値をとって各データを点として打つところは散布図と同じであるが、折れ線グラフではこれらの点を線で結ぶ。これにより \(x\) の値が増えたときの、\(y\) の値の連続的な変化を表現できる。
折れ線グラフのプロット例を以下に示す。
ノイズのない \(y = 2x\) の関係を表す2次元データ \((x, y)\) を sample_x、sample_y3 に用意し、その折れ線グラフを最初の散布図に重ねてプロットしている。
# プロットの入れ物の用意
fig, ax = plt.subplots(figsize=(5, 4))
sample_y3 = sample_x * 2
# 散布図、折れ線グラフのプロット
ax.scatter(sample_x, sample_y)
ax.plot(sample_x, sample_y3, color="orange")
# 表示
plt.show()
練習3
以下のコードにより、0から10までの0.1刻みの配列が x に、x のそれぞれの要素に対してsin関数の値を計算した配列が y_sin に、cos関数の値を計算した配列が y_cos に代入される。このとき x と y_sin、x と y_cos それぞれのペアについて折れ線グラフを作成することで、sin関数、cos関数を可視化しなさい。またそれぞれのプロットの区別がつくように "sin関数"、"cos関数" という凡例をつけなさい。
x = np.arange(0, 10, 0.1)
y_sin = np.sin(x)
y_cos = np.cos(x)
# プロットの入れ物の用意
fig, ax = plt.subplots(figsize=(5, 4))
# ここに適切なコードを書く
plt.legend() # 凡例の表示
# ファイルとして保存
plt.tight_layout()
plt.savefig("練習3.png")
# プロットの入れ物の用意
fig, ax = plt.subplots(figsize=(5, 4))
ax.plot(x, y_sin, label="sin関数")
ax.plot(x, y_cos, label="cos関数")
plt.legend() # 凡例の表示
# ファイルとして保存
plt.tight_layout()
plt.savefig("練習3.png")
プロットしたら以下のコードを実行することにより、画像をダウンロードできる。これを提出しなさい。
from google.colab import files
files.download("練習3.png")
注意として、ファイルとして保存する場合は plt.show() を実行してはいけない。これを実行してしまうと白紙の画像ファイルがダウンロードされる。